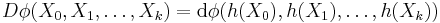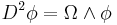Exterior covariant derivative

In mathematics, the exterior covariant derivative, sometimes also covariant exterior derivative, is a very useful notion for calculus on manifolds, which makes it possible to simplify formulas which use a principal connection.

Let P → M be a principal G-bundle on a smooth manifold M. If $\phi$ is a tensorial k-form on P, then its exterior covariant derivative is defined by

$D\phi(X_0,X_1,\dots,X_k)=\mathrm{d}\phi(h(X_0),h(X_1),\dots,h(X_k))$

where h denotes the projection to the horizontal subspace, 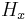$H_x$ defined by the connection, with kernel 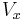$V_x$ (the vertical subspace) of the tangent bundle of the total space of the fiber bundle. Here 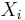$X_i$ are any vector fields on P. Dφ is a tensorial k+1 form on P.

Unlike the usual exterior derivative, which squares to 0, we have

$D^2\phi=\Omega\wedge\phi$

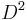where $\Omega$ denotes the curvature form. In particular $D^2$ vanishes for a flat connection.

References

Kobayashi, Shoshichi and Nomizu, Katsumi (1996 (New edition)). Foundations of Differential Geometry, Vol. 1. Wiley-Interscience. ISBN 0471157333.

Exterior covariant derivative

See also

References